Niver Strahler
E matematik, niver Strahler pe niver Horton–Strahler ur wezenn vatematek zo ur muzul niverel eus kemplezhded he brankadur.
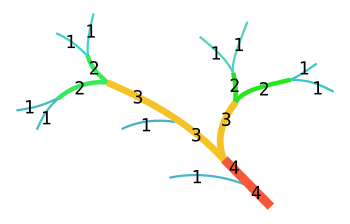
Implijet eo bet an niveroù-se da gentañ en hidrologiezh gant Robert E. Horton hag Arthur Newell Strahler. En degouezh-se e vezont anvet urzh dourredennoù Strahler hag implijet e vezont da dermeniñ ment an dourredennoù hervez hierarkiezh an adstêrioù. Implijet e vezont ivez e dielfennadur ar reizhadoù L hag ar frammoù biologel hierarkel e-giz reizhad analañ ha reizhad gwazhied ar gwez hag al loened, evit gouestlañ plas er rejistr e kompiladur ar yezhoù programmiñ a live uhel hag e dielfennadur ar rouedadoù sokial. Diorroet ez eus bet reizhadoù all da urzhiañ an dourredennoù gant Shreve[1][2], Hodgkinson et al.[3]. Ur geñveriadenn eus reizhadoù Strahler ha Shreve gant stadegoù, war un dro gant un dielfennadur eus hirderioù an dourredennoù/liammoù, zo roet gant Smart[4].
En hidrografiezh
kemmañAn niver Strahler zo 1 evit an holl dourredennoù etre o eienennoù hag o c'hemberadur kentañ[5].
Gwrizienn un dourredenn zo ar c'hemberadur el lec'h ma koll an dourredenn-se hec'h anv, da lâret eo, evit ur stêr vras, he genoù. Urzh un diazad doureier zo hini e zourredenn bennañ[5]. Gallout a ra ar rummatadur depantoud eus skeuliad ar gartenn implijet[6],[7].
Rummatadur an dourredennoù gant niver Strahler zo heverk-kenañ da gemer e kont framm ha stankder ar rouedad hidrografek[8]. Melezouriñ a ra kemmusted an degouezhioù hervez an douaroniezh (da skouer : hervez an hedreuzded eus substrad reier an diazad doureier) hag ar glavmetriezh dre e liamm strizh gant ar c'hementad dour kaset war c'horre an douar e-pad ar prantadoù kas bras[8].
Niver Strahler a dizh :
| Anv | Niver | |
|---|---|---|
| Stêr | Strahler[9] | Shreve |
| Amazon | 12 | 29 d’an nebeutañ |
| Mississippi | 10 | 23 d’an nebeutañ |
| Nil | 10 | 22 d’an nebeutañ |
| Ron | 9 | 20 d’an nebeutañ |
| Garonne | 9 | 16 d’an nebeutañ |
| Yenisey | 8 | 18 d’an nebeutañ |
| Danav | 8 | 15 d’an nebeutañ |
| Liger | 8 | 16 d’an nebeutañ |
| Kongo | 7 | 18 d’an nebeutañ |
| Indus | 7 | 19 d’an nebeutañ |
| Mekong | 7 | 19 d’an nebeutañ |
| Roen | 7 | 18 d’an nebeutañ |
| Seine | 7 | 16 d’an nebeutañ |
| Adour | 7 | 14 d’an nebeutañ |
| Dordogna | 7 | 14 d’an nebeutañ |
| Meuse | 7 | 14 d’an nebeutañ |
| Aar | 6 | 17 d’an nebeutañ |
| Oise | 6 | 16 d’an nebeutañ |
| Tavoez | 5 | 11 d’an nebeutañ |
| Tibre | 5 | 9 d’an nebeutañ |
| Marne | 5 | 14 d’an nebeutañ |
| Lot | 5 | 13 d’an nebeutañ |
Liamm diavaez
kemmañ- Javier Esparza, Michael Luttenberger ha Maximilian Schlund, "A Brief History of Strahler Numbers", 2014, Lec'hienn Skol-veur deknek Munchen.
Notennoù
kemmañ- ↑ Shreve, R.L., 1966. "Statistical law of stream numbers", Journal of Geology 74, 17–37.
- ↑ Shreve, R.L., 1967. "Infinite topologically random channel networks", Journal of Geology 75, 178–186.
- ↑ Hodgkinson, J.H., McLoughlin, S. & Cox, M.E. 2006. "The influence of structural grain on drainage in a metamorphic sub-catchment: Laceys Creek, southeast Queensland, Australia", Geomorphology, 81: 394–407.
- ↑ Smart, J.S. 1968, "Statistical properties of stream lengths", Water Resources Research, 4, No 5. 1001–1014
- ↑ 5,0 ha5,1 André Musy, Christophe, Higy, Hydrologie, Une science de la nature, Lausanne, 2004, pp.88 ha 89, (ISBN 2-88074-546-2).
- ↑ Denis Mercier, Géomorphologie de la France, Paris, 2013, p 248, (ISBN 978-2-10-059706-2).
- ↑ Réseau hydrographique : ordre des cours d’eau pour le réseau hydrographique numérique au 1:25 000 de la Suisse, www.bafu.admin.ch.
- ↑ 8,0 ha8,1 "Typologie des cours d’eau de France métropolitaine", p. 12, Cemagref.
- ↑ Colbert E. Cushing, Kenneth W. Cummins, G. Wayne Minshall, River and Stream, Londrez, 2006, p. 390, (ISBN 0-520-24567-9)